fa66
Aktives Mitglied
- Dabei seit
- 16.04.2009
- Beiträge
- 20.074
- Reaktionspunkte
- 9.741
Hmm?Eben nicht.1:2 = 0,5
Wenn ich 1 Apfel auf 2 Personen (
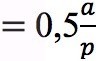 )
)Das ändert sich aber auch nicht, wenn ich es so notiere:
Es bleibt beim halben Apfel. Nach deiner Argumentation sei aber:
Ändert sich durch die Notation etwas an der Äpfelizität des Apfels? Oder was habe ich da sonst falschverstanden?