Mathe-Aufgabe ("Exponential- und Logarithmusaufgaben")

[BGY]

noch eine Mathe-Aufgabe! ("Exponential- und Logarithmusaufgaben")

Ich beiss mir nun schon ne ganze Weile an dieser Aufgabe die Zähne aus:

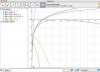
Ziehe vom Ursprung aus die Tangente an die Kurve y=ln x und bereche die Koordinaten des Brührpunktes.

Kann mir vielleicht jemand sagen, wie ich diese Aufgabe lösen muss?

Die Lösung, auf die ich kommen sollte, ist P(e/1).

Wers weiss, kriegt nen Kuchen!

 

[Zapfenzieher]

Differential bilden: D ln(t) = 1/t

Tangente an ln im Punkt t hat die Form: y(x)=1/t*x+b

Tangente geht durch den Ursprung: 0=y(0)=b

Tangent hat somit Form y(x)=1/t*x.

Im Schnittpunkt gilt x=t und Tangente beruehrt ln, also folgt y(t)=1=ln(t)

Aus 1=ln(t) folgt e=t.

 

[BGY]

Danke für die schnelle Antwort. Allerdings ist mir die Aufgabe immer noch nicht ganz klar.

Tangente an ln im Punkt t hat die Form: y(x)=1/t*x+b

y(x)=(1/t)*t+b oder y(x)=1/(t*x)+b?

Im Schnittpunkt gilt x=t und Tangente beruehrt ln, also folgt y(t)=1=ln(t)

Vom "und" an komm ich nicht mehr wirklich nach... Warum ist jetzt y(t)=1?

Danke

 

[Sir_RamDac]

y(x)=(1/t)*t+b oder y(x)=1/(t*x)+b?

y(x)=(1/t)*x+b

Der Anstieg der Geraden und der Funktion (im 'Schnittpunkt') sind gleich.

Vom "und" an komm ich nicht mehr wirklich nach... Warum ist jetzt y(t)=1?

y(t)=(1/t)*t = 1

 

[Mabbel]

Also ich hatte ja auch grade Logarithmen in der Schule, aber sowas ist mir noch nicht untergekommen =)

Nur mal so aus Interesse - welche Klasse und welche Schulart bist du?

 

[Zapfenzieher]

Das ist auch keine Aufgabe um Logarithmen sondern um Differentialrechnung zu üben.

Logarithmen werden viel früher behandelt als die Differentialrechnung.

Der Logarithmus hier war einfach nur Teil des Beispiels. Analog hätte man auch irgend eine andere Funktion nehmen können.

 

[BGY]

Danke für alle Antworten, jetzt geht es! War wohl auch schon ein wenig müde gestern...

Also ich hatte ja auch grade Logarithmen in der Schule, aber sowas ist mir noch nicht untergekommen =)

Nur mal so aus Interesse - welche Klasse und welche Schulart bist du?

Ich bin in der 4. Kanti aka Kantonsschule aka Gymnasium. Dieses Jahr hab ich die Matura, und das ist eine von 100 Übungsaufgaben, die der Lehrer für die mündliche Matura verteilt hat.

Das ist auch keine Aufgabe um Logarithmen sondern um Differentialrechnung zu üben.

Logarithmen werden viel früher behandelt als die Differentialrechnung.

Eigentlich ist es eine Aufgabe, um beides zu üben. Jetzt wird halt alles, was wir je durchgenommen haben, in einen Topf geworfen, und die Aufgabe ist wohl unter "Exponential- und Logarithmusfunktionen" zu finden, weil es sich um eine Logarithmusfunktion handelt.

Ps: Ich sitz grad an nem Win-Rechner und hab grad gemerkt, wie nützlich die Mac-weite Rechtschreibeprüfung ist. Hab ich gar nie richtig bemerkt, als ich sie nutzte!

 

[Heavok]

Hachja, bin ich froh, dass ich mathe nicht im abi hab

Mfg, Heavok

 

[Sir_RamDac]

Hachja, bin ich froh, dass ich mathe nicht im abi hab

Mfg, Heavok

Wie kann man denn Mathe nicht im Abi haben

 

[Fabi87]

schweinerei......und ich lern das gerade wie blöd?!?!?

 

[janpi3]

Wie kann man denn Mathe nicht im Abi haben

Er könnte zum Beispiel eine Ersatzarbeit schreiben.

 

[BGY]

So, jetzt hab ich nochmals eine, an der ich mir die Zähne ausbeisse:

F¨r welche Werte von m hat die Gleichung mx+2=ln(x) genau eine Lösung für x?
Hinweis: Überlege anhand einer Figur.

y=ln(x) hat für x=>(unendlich) keine Asymptote und wächst langsamer als y=x, dh. m[grösser/gleich]0.

Ich komm einfach nicht dahinter...

Ach ja: Bitte lieber zwei, drei Wörter ausführlicher sein bei der Antwort und nicht so wenig schreiben wie möglich!

Danke

 

[janpi3]

Fauler Sack.

 

[macintosh85]

Deine Musterlösung stimmt ja schonmal nicht.

 

[BGY]

Deine Musterlösung stimmt ja schonmal nicht.

Aha. Und wie kommst du darauf?

Ich bin nicht der beste Gedankenleser, zumal übers Internet...

 

[Sir_RamDac]

Aha. Und wie kommst du darauf?

Weil die Gleichung fuer m>=0 auch zwei Loesungen haben kann..

 

[Zapfenzieher]

Fall 1: M=0

Offensichtlich genau eine Loesung: e^2

Fall 2: M<0:

Der Logarithmus ist eine streng monoton wachsende Funktion.

Wiederum existiert genau eine Lösung. Denn mx+2 ist für m<0 streng monoton fallend. Mehrere Schnittpunkte oder kein Schnittpunkt würden zu einem Wiederspruch führen (klar, oder?).

Fall 3: M>0 (hier wird es interessant)

In einem allfälligen ersten Schnittpunkt muss die Steigung der Geraden kleinergleich (<=) der Steigung des Logarithmus sein, da die Gerade ja oberhalb des Logartihmus beginnt.

D(mx+2) = m <= D ln(x) = 1/x also x <= 1/m.

Der erste Schnittpunkt muss also sicher vor oder bei 1/m liegen.

Ich muss jetzt los, löse sie heute Abend oder so fertig.

 

[walfreiheit]

Wenn ich den Murks wieder sehe wird mir schlecht!
Bin ich froh, dass ich damit schon lange nichts mehr zu tun habe.

 

[BGY]

Danke für die Erklärung, @Zapfenzieher!

 

[neptun]

mx+2=ln(x) hat genau eine Lösung genau dann, wenn der Graph der Funktion definiert durch f_m(x)=ln(x)-mx-2 die x-Achse genau ein Mal schneidet.

Also würde ich die Funktionenschar definiert durch f_m(x)=ln(x)-mx-2 untersuchen.

Ableitung: f_m'(x)=1/x-m

m<0: Ableitung ist immer positiv, also Funktion monoton wachsend; man erhält genau einen Schnittpunkt mit der x-Achse

m=0: dies ist der bereits erwähnte Spezialfall; ebenfalls genau ein Schnittpunkt

m>0: die Ableitung wird 0 bei 1/m, und f(1/m)=-ln(m)-3; also sind (1/m;-ln(m)-3) die Koordinaten des Maximums
* für m=1/(e^3) liegt dieses Maximum auf der x-Achse, also ebenfalls genau eine Lösung
* 0<m<1/(e^3): 2 Lösungen
* m>1/(e^3): keine Lösung

Die Grafik zeigt die Fälle m=-1, m=0, m=0.01, m=1/(e^3), m=0.5, m=1; der 2te Schnittpunkt im Fall m=0.01 ist auf dem Ausschnitt nicht mehr sichtbar